The Theory Of
Relativity is a combination or we can say that is basically a set of
two theories in physics: special relativity and general relativity. The
core idea of both theories is that two observers who move relative to
each other will often measure different 'time' and 'space' intervals for
the same events, but the content of physical law will be the same for
both. It says that time and lengths are no longer absolutes. You’ve
placed your digital watch on your wrist and a meter ruler on your desk.
These seem like absolutes: a second and a centimeter for you must be the
same as they are for me, and the same as they are on Alpha Centauri.
But they’re not.
There are several different theories of relativity, but there is one that is most commonly used. Albert Einstein created the most commonly known today Theory of Relativity which was later used to develop the atomic bomb. This theory (E=mc2) is probably his most well known work and used all the time in everyday science. This theory of relativity is split into two different parts, the General Theory of Relativity and the Special Theory of Relativity. Albert Einstein says he thought of his Special Theory of Relativity by looking at both Maxwell and Lorentz electrodynamics equations. Both of their equations were believed to be correct however they contradicted the additional rule of velocity used in mechanics. Einstein managed to change Lorentz equation so that it fit with the rule by using time. By using time both Maxwell's and Lorentz's equations were made correct thus allowing him to create the Special Theory of Relativity.
Just recently, French scientists French Centre for Theoretical Physics have proven that E= mc2 is true and has been resolved at the scale of subatomic particle level. Protons and neutrons are made of quarks which are bound together by gluons. The mass of the gluons is 0% and the mass of the quarks are 5% but there's still 95% missing from the total. This is actually true because the mass is equal to the energy. After 103 years, we have can finally understand what Einstein was saying and know that its true due to some supercomputers and a team of scientists proving that he was a century ahead of his time.
There are several different theories of relativity, but there is one that is most commonly used. Albert Einstein created the most commonly known today Theory of Relativity which was later used to develop the atomic bomb. This theory (E=mc2) is probably his most well known work and used all the time in everyday science. This theory of relativity is split into two different parts, the General Theory of Relativity and the Special Theory of Relativity. Albert Einstein says he thought of his Special Theory of Relativity by looking at both Maxwell and Lorentz electrodynamics equations. Both of their equations were believed to be correct however they contradicted the additional rule of velocity used in mechanics. Einstein managed to change Lorentz equation so that it fit with the rule by using time. By using time both Maxwell's and Lorentz's equations were made correct thus allowing him to create the Special Theory of Relativity.
Just recently, French scientists French Centre for Theoretical Physics have proven that E= mc2 is true and has been resolved at the scale of subatomic particle level. Protons and neutrons are made of quarks which are bound together by gluons. The mass of the gluons is 0% and the mass of the quarks are 5% but there's still 95% missing from the total. This is actually true because the mass is equal to the energy. After 103 years, we have can finally understand what Einstein was saying and know that its true due to some supercomputers and a team of scientists proving that he was a century ahead of his time.
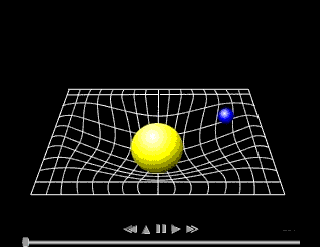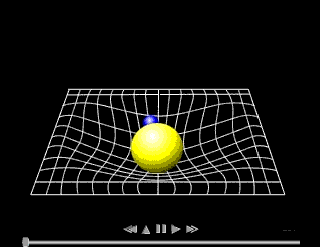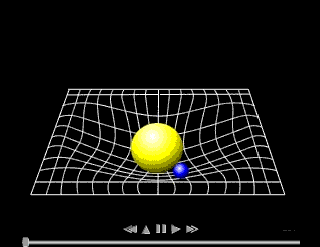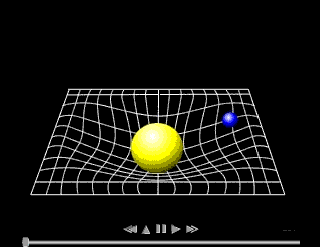
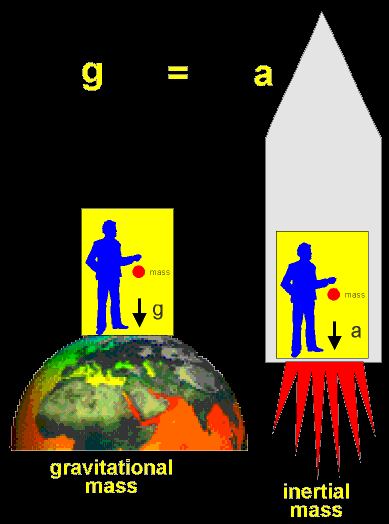
General
relativity was published by Einstein in 1916. It uses the mathematics
of differential geometry and tensors in order to describe gravity. The
laws of general relativity are the same for all observers, even if they
are accelerated with respect to each other. General relativity is a
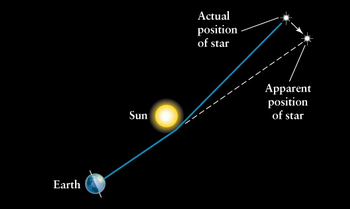
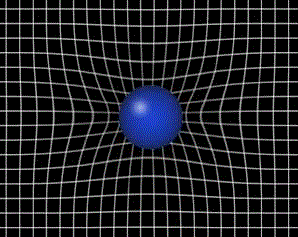
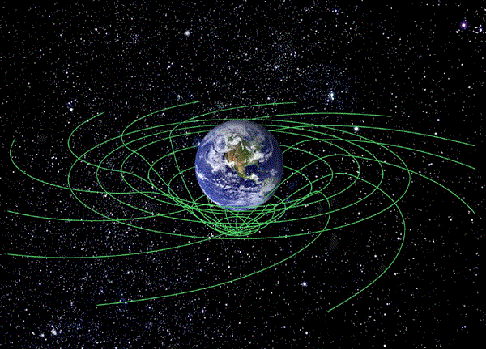
geometrical theory which postulates that the presence of mass and energy
"curves" space, and this curvature affects the path of free particles
(and even the path of light), an effect we interpret as a gravitational
force.
The
theory can be used to build models of the evolution of the universe and
is hence a crucial tool in cosmology. The General Theory of Relativity
is one of the two of Einstein's Theories of Relativity. The General
Theory of Relativity is the same thing as the special theory of
relativity, however includes gravity and eliminates that "restricted"
portion of the General Theory of Relativity, thus improving the Special
Theory of Relativity to the General Theory of Relativity.
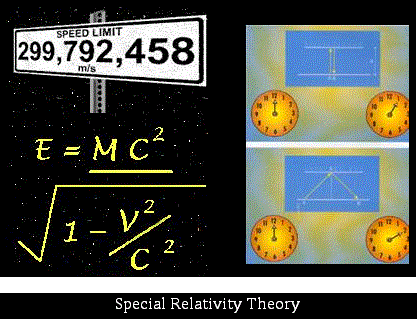
The
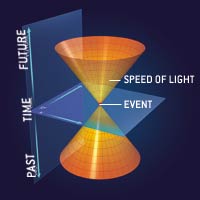
speed of light emerges as an upper limit for the speed of matter and
information. Mass and energy are seen as equivalent. Two events judged
to be simultaneous by one observer may be seen as non-simultaneous by
other observers which are in motion with respect to the first one. The
theory does not account for gravitational effects. The mathematical
basis of special relativity is provided by the Lorentz
transformation.The General Theory of Relativity is one of the two of
Einstein's Theories of Relativity. The General Theory of Relativity is
the same thing as the special theory of relativity, however includes
gravity and eliminates that "restricted" portion of the General Theory
of Relativity, thus improving the Special Theory of Relativity to the
General Theory of Relativity.
General
relativity was published by Einstein in 1916. It uses the mathematics
of differential geometry and tensors in order to describe gravity. The
laws of general relativity are the same for all observers, even if they
are accelerated with respect to each other. General relativity is a
geometrical theory which postulates that the presence of mass and energy
"curves" space, and this curvature affects the path of free particles
(and even the path of light), an effect we interpret as a gravitational
force.
The
theory can be used to build models of the evolution of the universe and
is hence a crucial tool in cosmology. The General Theory of Relativity
is one of the two of Einstein's Theories of Relativity. The General
Theory of Relativity is the same thing as the special theory of
relativity, however includes gravity and eliminates that "restricted"
portion of the General Theory of Relativity, thus improving the Special
Theory of Relativity to the General Theory of Relativity.
The
speed of light emerges as an upper limit for the speed of matter and
information. Mass and energy are seen as equivalent. Two events judged
to be simultaneous by one observer may be seen as non-simultaneous by
other observers which are in motion with respect to the first one. The
theory does not account for gravitational effects. The mathematical
basis of special relativity is provided by the Lorentz
transformation.The General Theory of Relativity is one of the two of
Einstein's Theories of Relativity. The General Theory of Relativity is
the same thing as the special theory of relativity, however includes
gravity and eliminates that "restricted" portion of the General Theory
of Relativity, thus improving the Special Theory of Relativity to the
General Theory of Relativity.
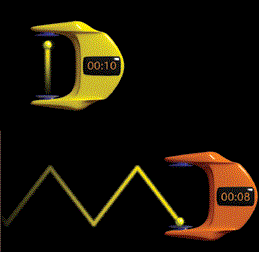
Einstein's
theory of special relativity is that the length of objects moving at
relativistic speeds undergo a contraction along the dimension of motion.
An observer at rest (relative to the moving object) would observe the
moving object to be shorter in length. That is to say, that an object at
rest might have be measured to be 200 feet long; yet the same object
when moving at relativistic speeds relative to the observer/measurer
would have a measured length which is less than 200 ft. This phenomenon
is not due to actual errors in measurement or faulty observations; the
object is actually contracted in length as seen from the stationary
reference frame.
The
amount of contraction of the object is dependent upon the object's
speed relative to the observer. Note that the length contraction is only
significant when the object is moving at relativistic speeds - i.e.,
speeds which are a significant fraction of the speed of light.
Furthermore, note that the contraction only occurs in the dimension of
the object's motion. That is, if the object is moving horizontally, then
it is the horizontal dimension which is contracted; there would be no
contraction of the height of the object.
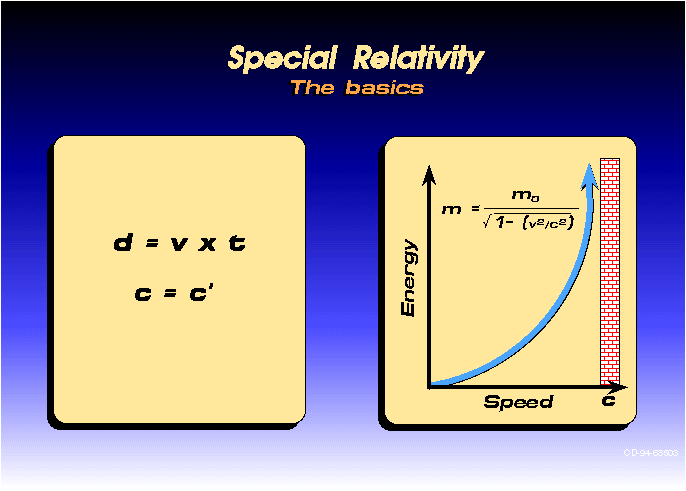
Because
it can? Not quite. Suppose Jim takes off in a spaceship leaving Bob
behind. Jim has his spaceship set on constant thrust mode, so that the
force of the engines pushing his spaceship forward is always the same.
This makes Jim accelerate; he is always going faster and faster. But as
we all know, the fastest Jim can ever go is the speed of light. So how
can he always be going faster and faster?
Jim
approaches the speed of light asymptotically, meaning he always is
moving toward it, but never quite reaches it. His acceleration decreases
the faster he goes, even though he is always accelerating. His
acceleration will eventually be very small, but it will never be zero.
"But",
says you, "physics tells us the Force = Mass x Acceleration, and you
said Jim's spaceship's engines were always exerting the same force on
the spaceship." And you are correct to point this out. Since f = ma, and
f stays the same while a decreases, m, Mass, must increase. And it
does. Look at the following graph:
Since
Mass approaches infinity, and Jim's thrust is constant, his
acceleration will approach zero. If Jim wanted his acceleration to be
constant, he would have to increase his thrust at the same rate at which
his mass was increasing. This is very hard, since the thrust required
to accelerate him would also approach infinity.
Adding Velocities in Relativity
In netwonian physics, you just added velocities.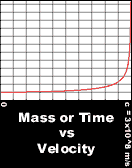
Let's call
w the velocity observed by Bob.
u the velocity of the train.
v the velocity of Jim walking inside the train.
c, of course, the velocity of light.
Here's the formula: w =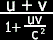
If
you plug in all the numbers, you calculate that Bob sees Jim moving at
90.91% the speed of light. Of course, the difference between Newtonian
physics and relativistic physics is only significant at very high
velocities.
Where e=mc2 Comes From
Everyone
knows the equation, but few know why it comes from relativity or how to
derive it. Let's take a look at the equation for mass:
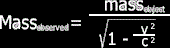
We can re-write this equation like this (replacing M' for Observed Mass and M for the mass of the object at rest):
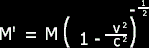
We can expand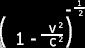 
using the binomial theorem just like we can expand (a+b)2 into a2
+ 2ab + b2. As it turns out, when you expand 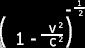you end up with an infinite series. But the
= 
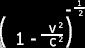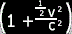
We can put the expanded version back into our mass equation:
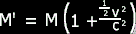
Distribute the M: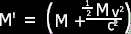
A really cool thing happened, (maybe you noticed). In physics, we use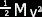 
all the time to represent the energy of a moving body. So, e = 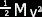(Piece of cake.) Now we can substitute it in our equation.
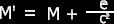
You
can express the difference between something's rest mass and its
observed mass with (M' - M). We'll call this difference in mass m. The
rest of the derivation becomes obvious, and you have no other choice
than to come up with e = mc²
The Math Behind General Relativity
The math behind general relativity is called Einstein Field Equations. They are equations of the coupled hyperbolic-elliptic nonlinear partial differential type, which, in plain English, means that they are really, really hard. Einstein himself recognized the mathematical difficulties of general relativity as "very serious." He predicted it as being the primary hindrance of general relativity's development. The equation can be stated in a "symbolic form" that isn't very useful. Here it is:
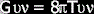
It
doesn't mean much to us, but you can see on the left of the equal sign
the stuff that describes the curvature of space-time. On the right is
the matter within space-time, and how it behaves.
In netwonian physics, you just added velocities.
For
example, let's say Jim is on a train and Bob is on the side of the
track. The train is going 50 miles per hour. Jim walks forward inside
the train at 3 miles per hours relative to the train. In Newton's model
of the universe, Bob would observe Jim moving at 53 miles per hour,
because 50 + 3 = 53.
Newtonian
physics breaks down at very high velocities, because if one simply
added velocities, the result might very well exceed the speed of light.
If the train in the previous example we moving at 75% the speed of
light, and Jim walks forward at 50% the speed of light (a very rare feat
indeed), Newtonian physics says he's going 125% the speed of light.
The
trick is to realize that Bob see's Jim in slow motion. When Jim thinks
he's running along the inside of the train at 50% the speed of light,
Bob sees him as moving much slower.
Let's call
w the velocity observed by Bob.
u the velocity of the train.
v the velocity of Jim walking inside the train.
c, of course, the velocity of light.
Here's the formula: w =
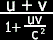
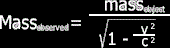
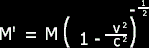
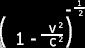using the binomial theorem just like we can expand (a+b)2 into a2 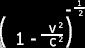you end up with an infinite series. But the infinite
series is such that each term is less significant than the term before
it. So we just need to look at the significant parts to get an
aproximation: the first two terms. We end up with something like this:
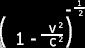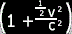
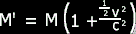
= Distribute the M:
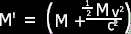
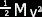all the time to represent the energy of a moving body. So, e = 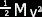(Piece of cake.) Now we can substitute it in our equation.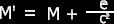 The math behind general relativity is called Einstein Field Equations. They are equations of the coupled hyperbolic-elliptic nonlinear partial differential type, which, in plain English, means that they are really, really hard. Einstein himself recognized the mathematical difficulties of general relativity as "very serious." He predicted it as being the primary hindrance of general relativity's development. The equation can be stated in a "symbolic form" that isn't very useful. Here it is:
