The Fibonacci numbers are Nature's numbering system. They appear everywhere in Nature, from the leaf arrangement in plants, to the pattern of the florets of a flower, the bracts of a pinecone, or the scales of a pineapple. The Fibonacci numbers are therefore applicable to the growth of every living thing, including a single cell, a grain of wheat, a hive of bees, and even all of mankind.
Stan Grist
http://www.stangrist.com/fibonacci.htm
Stan Grist
http://www.stangrist.com/fibonacci.htm
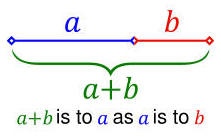
Golden Ratio & Golden Section : : Golden Rectangle : : Golden Spiral
Golden Ratio & Golden Section
In mathematics and the arts, two quantities are in the golden ratio if the ratio between the sum of those quantities and the larger one is the same as the ratio between the larger one and the smaller.
Expressed algebraically:
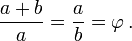
The golden ratio is often denoted by the Greek letter phi (Φ or φ).
The figure of a golden section illustrates the geometric relationship that defines this constant. The golden ratio is an irrational mathematical constant, approximately 1.6180339887.
The figure of a golden section illustrates the geometric relationship that defines this constant. The golden ratio is an irrational mathematical constant, approximately 1.6180339887.
Golden Rectangle
A golden rectangle is a rectangle whose side lengths are in the golden ratio, 1: j (one-to-phi), that is, 1 : or approximately 1:1.618.
A golden rectangle can be constructed with only straightedge and compass by this technique:
Construct a simple square
A golden rectangle can be constructed with only straightedge and compass by this technique:
Construct a simple square
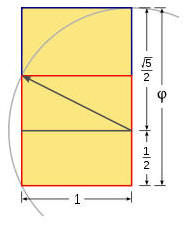
Draw a line from the midpoint of one side of the square to an opposite corner
Use that line as the radius to draw an arc that defines the height of the rectangle
Complete the golden rectangle

